Why do ResNets and Inception Module work?
Problem of very deep CNNs
In recent years, CNNs have become deeper, with state-of-the-art networks going from just a few layers (e.g., AlexNet) to over a hundred layers.
The main benefit of a very deep network is that it can represent very complex functions. It can also learn features at many different levels of abstraction, from edges (at the lower layers) to very complex features (at the deeper layers). However, using a deeper network doesn’t always help.
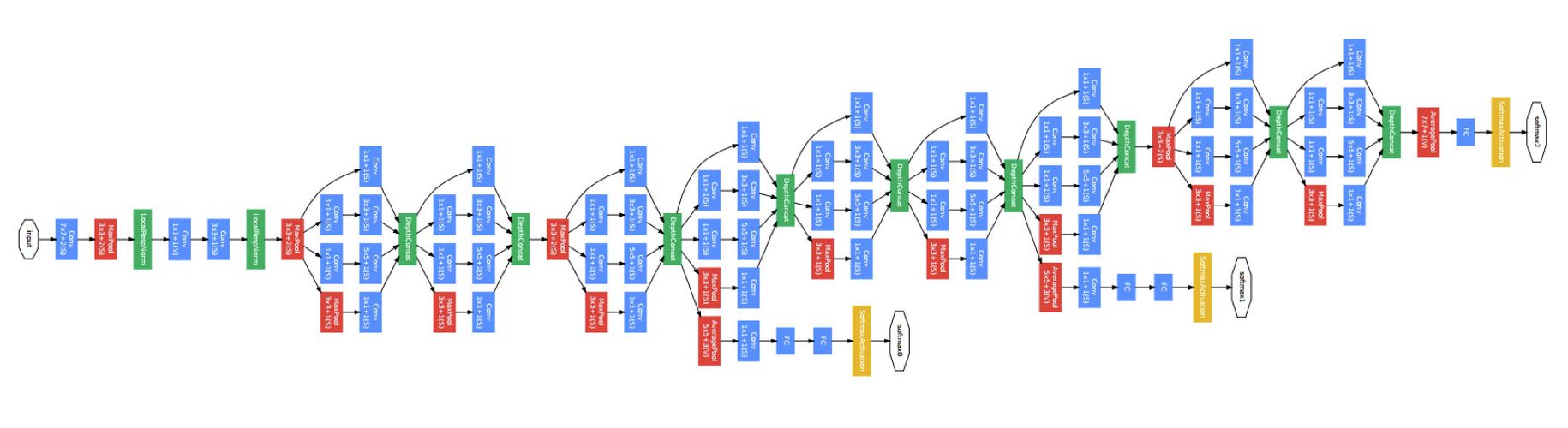
A huge barrier to training them is vanishing gradients: very deep networks often have a gradient signal that goes to zero quickly, thus making gradient descent unbearably slow. More specifically, during gradient descent, as you backprop from the final layer back to the first layer, you are multiplying by the weight matrix on each step, and thus the gradient can decrease exponentially quickly to zero
During training, you might therefore see the magnitude (or norm) of the gradient for the earlier layers decrease to zero very rapidly as training proceeds:
TLDR: The speed of learning decreases very rapidly for the early layers as the network trains, due to vanishing gradient.
Resnet blocks

Three reasons why resnet blocks work:
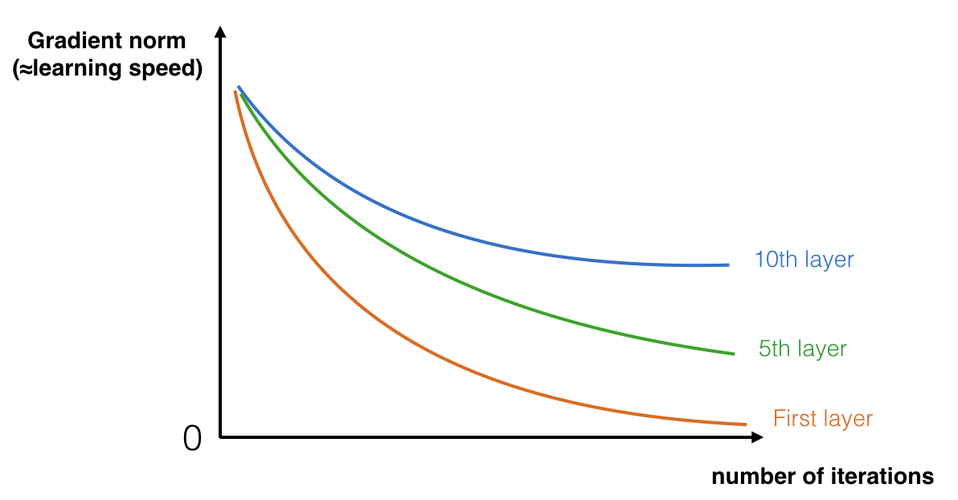
- The shortcut makes it very easy for one of the blocks to learn an identity function (where the network learns to behave exaclty like the one without skip-connection). So, ResNet blocks can be stacked on top of each other with little risk of harming training set performance. In plain nets, as we go deeper and deeper in the network, the layers fail to learn even the basic identity function and tend to perform worse.
- The shortcut or “skip-connection” allows the gradient to be directly back-propagated to earlier layers which reduces vanishing gradient problem a bit.
- Doing well on the training set is a pre-requisite for doing well on the hold-out crossvalidation set. In plain nets, as the number of layers increase, the training error increases significantly after some point. Skip-connections solve this problem where training error strictly decreases.
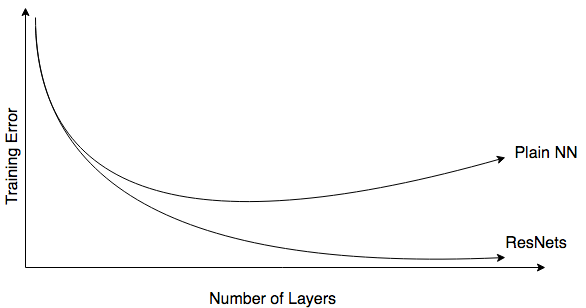
Resnet 50
Resnet 50 is divided into 5 stages.
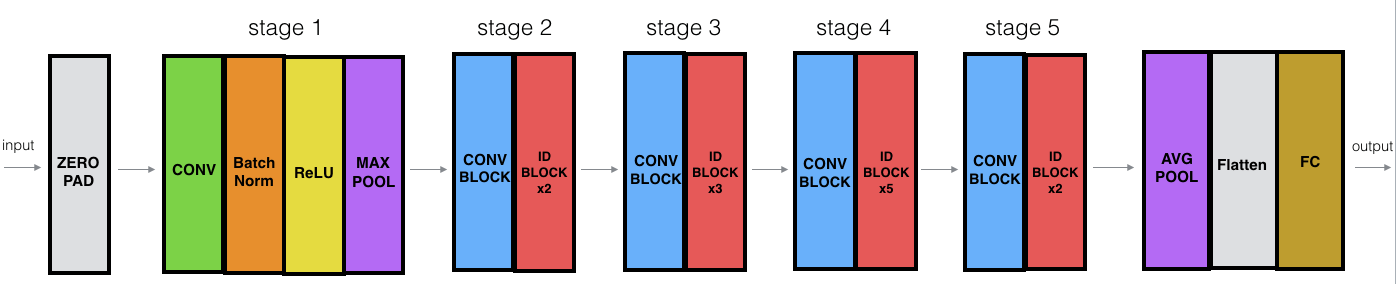
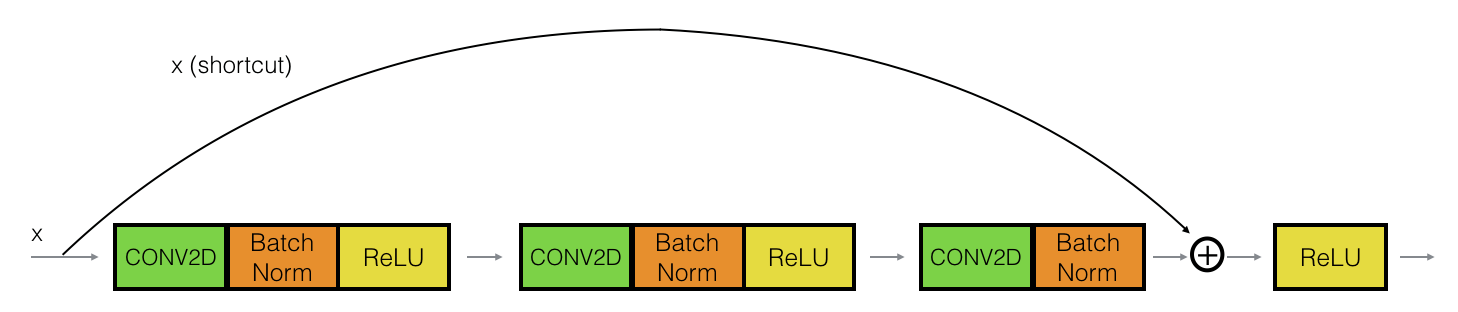
which comprises of identity block:
and convolution block:
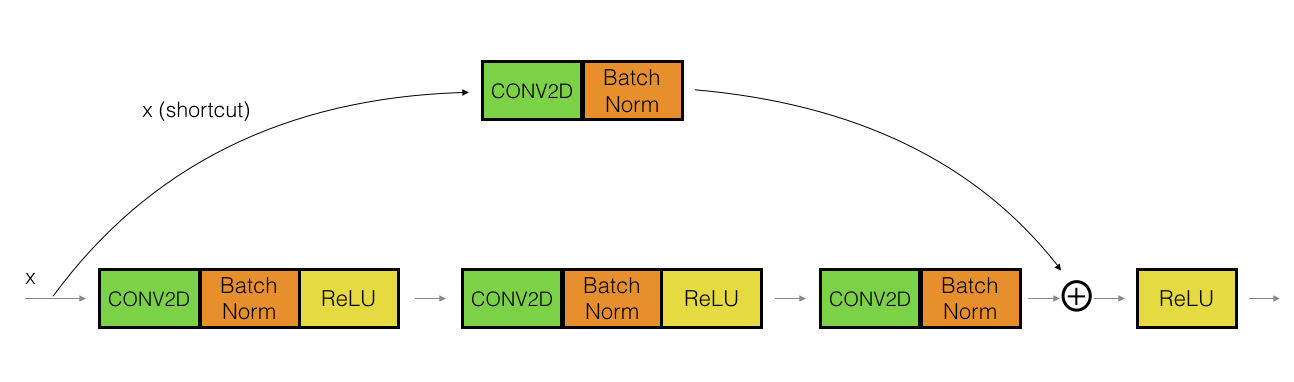
Identity block is used when the input(x) and output have the same dimensions. Convolution block is used when the input(x) and output don’t have the same dimensions. Shortcut path is used to change the dimension of input to that of the output.
Implementation of Resnet-50 on SIGNS dataset can be found here
Inception module
-
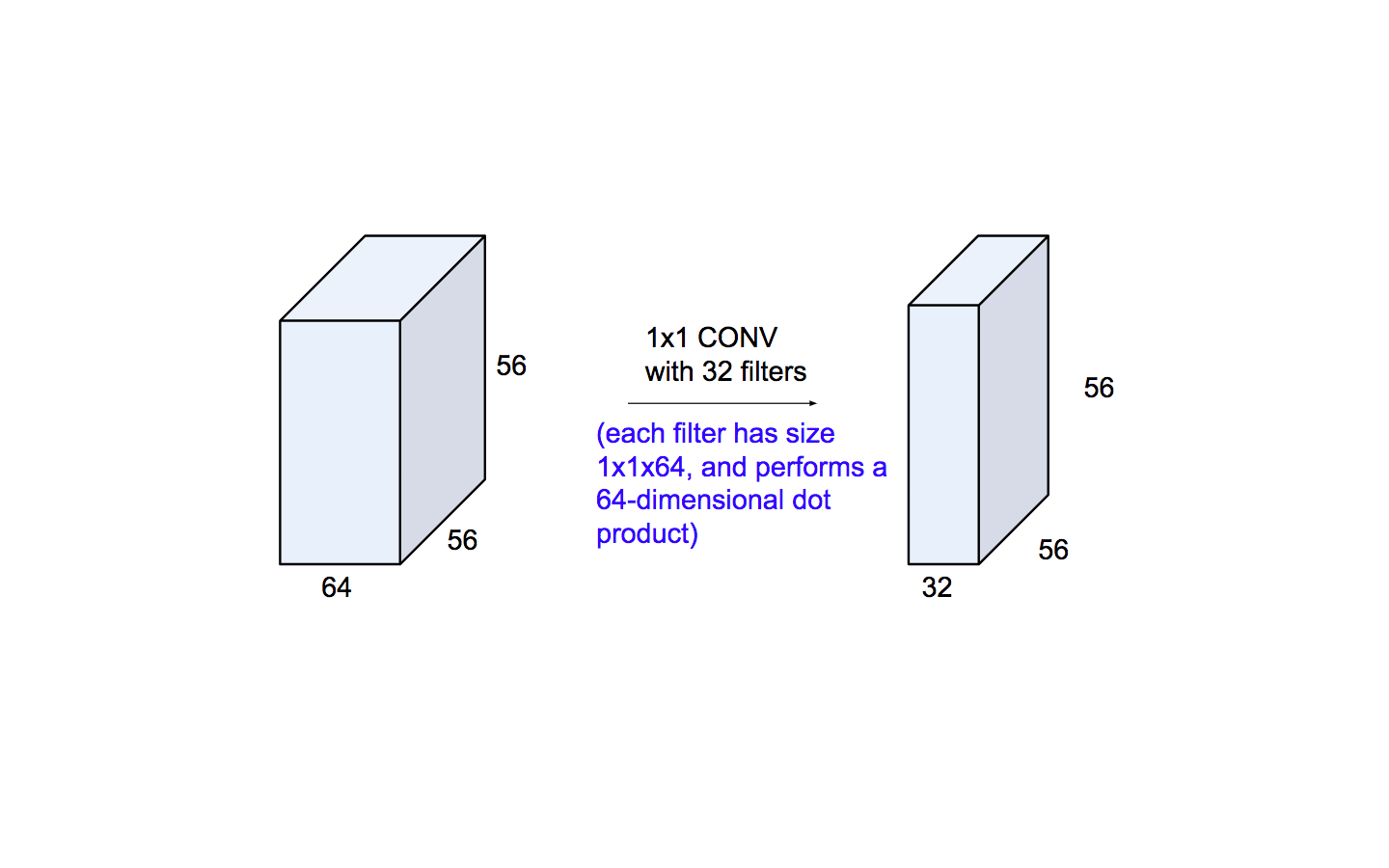
Network in Network Layers (1x1 convolution)
Now, at first look, you might wonder why this type of layer would even be helpful since receptive fields are normally larger than the space they map to. However, we must remember that these 1x1 convolutions span a certain depth, so we can think of it as a 1 x 1 x N convolution where N is the number of filters applied in the layer. They are also used as a bottle-neck layer which internally is used to decrease the number of parameters to be trained, and hence reduces the total computation time.
Dimensionality reduction:
- Height and Width : Max-pooling
- Depth : 1x1 convolution
-
Computation time
Total computation time = (Number of muliplies needed to compute one output value) x (Number of output values that need to be computed)
Consider two scenarios:
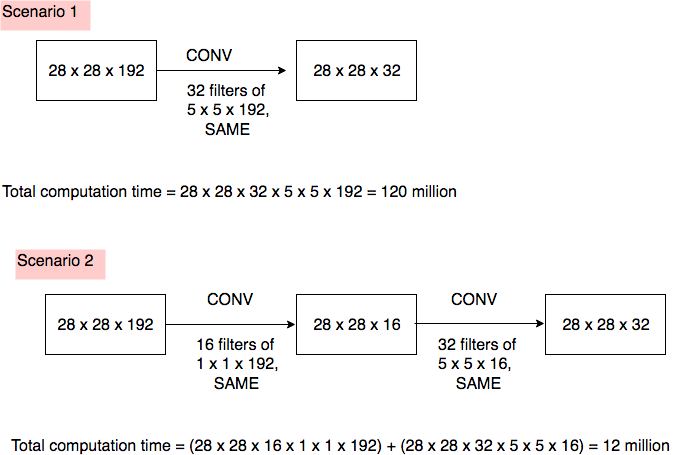
Introducing a 1x1 convolution brings down the total computation time by 10x
-
Inception block
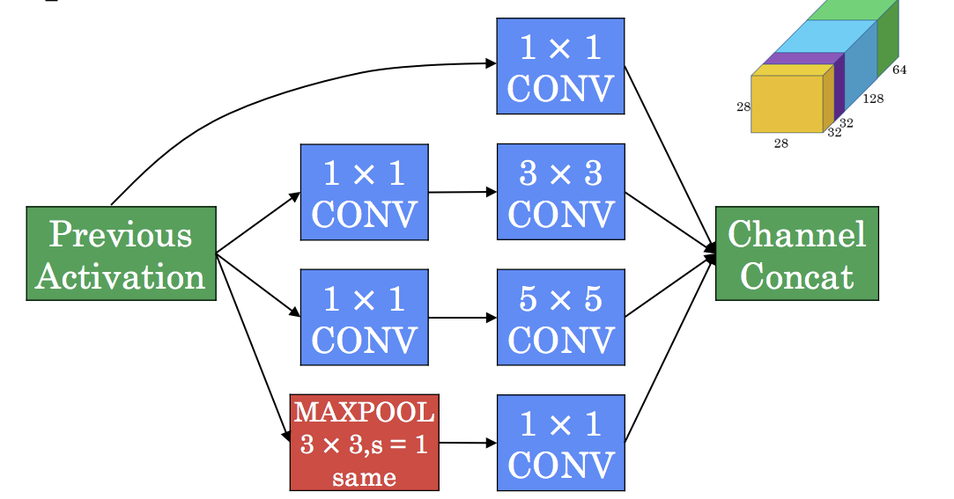
1x1 convolutions before 3x3 and 5x5 are used as a bottleneck layer.
1x1 convolutions after maxpool is used to reduce the depth of image.
At the end, all outputs are concatenated to produce a huge monolithic activation. The overall idea is to try all types of filters instead of 1 filter.
Entire inception network comprises of inception blocks as above, stacked after one other